Drop7AI

Drop7 - Rules and Strategy

Rules

The game is played on a 7x7 square grid. In each round, the player places a disc that falls from the top of the grid. Each disc has a number 1-7. Whenever the number of any disc matches the number of contiguous discs in a row or column, that disc disappears and also hits any blank discs it touches. When a blank is hit twice, it turns into a numbered disc. After 5 turns, the round ends and a full row of blank discs emerges from the bottom of the grid. The objective is to eliminate discs for as long as possible until the grid overflows.

Wikipedia

Strategy

A beginner in the game of Drop7 will try to remove as many discs as he can without thinking ahead. After several games some patterns may emerge; for example: a 7 disc contiguous to a 1 disc. The only way you can destroy the 1 is to first destroy the 7. The 7 will be destroyed only if an entire row or column is filled. To create a full column is easy, but doing so will waste discs that could help destroy blank discs. Completing a full row is hard, because most of the time the row will be fragmented. If we ignore these discs, the columns they sit on will tower and overflow the grid. This example shows how this game has no simple answers/strategy to maximize your score.

Genetic Algorithm

Implementation And Evolution


Implementation

Programming Language

I decided to rewrite the game in C on my personal computer as it provided me with an easy interface between the AI and the game.
Moreover I choose C and not a scripted language (e.g. Python) because of the significant speed difference in execution time.

Initialization and Process

In order to create a Genetic Algorithm an initial population of programs is created; for each program, we create a tree of random functions and values (values can only be in the leaves of the tree - Fig.1).
After the initialization process is completed, each program plays 100 games. The number 100 has no particular meaning and was chosen as a large enough number to remove an element of luck in the program's ability to win. After all games have concluded, a sorting algorithm is performed and the best programs are combined. The resulting combination is written over the worst programs (for more see the Evolution section). Each time this process is completed we get a new generation of programs. This process is done many times and the results per generation can be seen in the Results vs. Expectations section.

Figure 1: A Genetic Program tree representing max(x+x,x+3*y) [1]

Evolution



DNA

The DNA of each program is the functions and values it can choose from in order to create itself. The functions that I created for the AI to use are shown in Tb.1.The values it can choose from are shown in Tb.2, notice that values can only be leaves in the program tree (Fig.1)




Selection

First, we need to decide on parameters of defining the best programs, so we could combine them and hopefully get even better programs. A naïve approach would be to choose the programs that passed the most rounds. Although doing so would improve on the initial (purely random[2]) program, the AI will quickly converge to a local maximum. The reason for this is the risk of there being no deviation between programs.
Essentially, the problem we want to avoid is the programs turning into clones of each other.
In order to force deviation between programs I created 100 random boards. Each program determines its next move for each board. If the program selected a move that most programs didn't, its deviation score increases by 1. Thus each program can get a deviation score between 0 to 100.





Reproduction

Reproduction is done by combining the best programs with each other. The population is sorted by a combination of the devation_score and the max_reward and the 20 programs with the best combined score are chosen. Subsequently, each of these programs are combined with the program that succeeds it. The combination process is done randomly (Fig.2)) and the outcomes (offspring) are written over the 20 worst programs from the previous generation.
The combination process works by chance; there is a 50% chance that the male program will deliver its function and a 50% that the female program will. In addition to every passing of function there is a 1% chance for the function to change entirely by mutation.

Functions

GetNumberOfDiscsinPartRow(int)

CheckIfLastDiscIsBlock(int)

g_ai_main_board(int, int)

Sum(int, int)

Subtract(int, int)

SafeDivision(int, int)

Multiply(int, int)

IfLargerThenInc(int, int)

IfEqual(int, int)
Table 1: Function List


Values

curr->val

col_pos

row_pos

g_curr_disc
Table 2: Value List


Figure 2: Example of a combination of programs with different sizes and shapes[3]

Results vs. Expectations



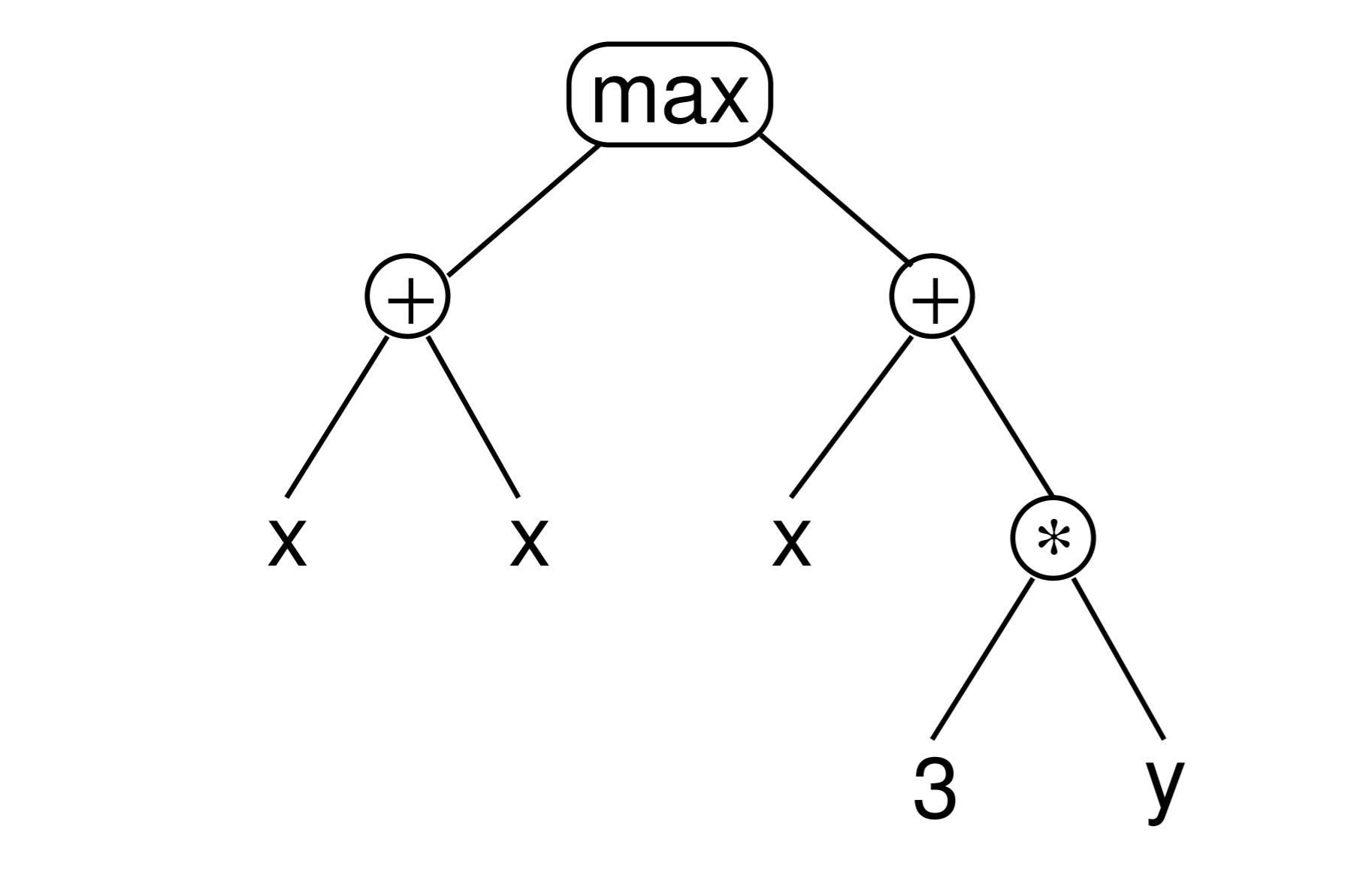
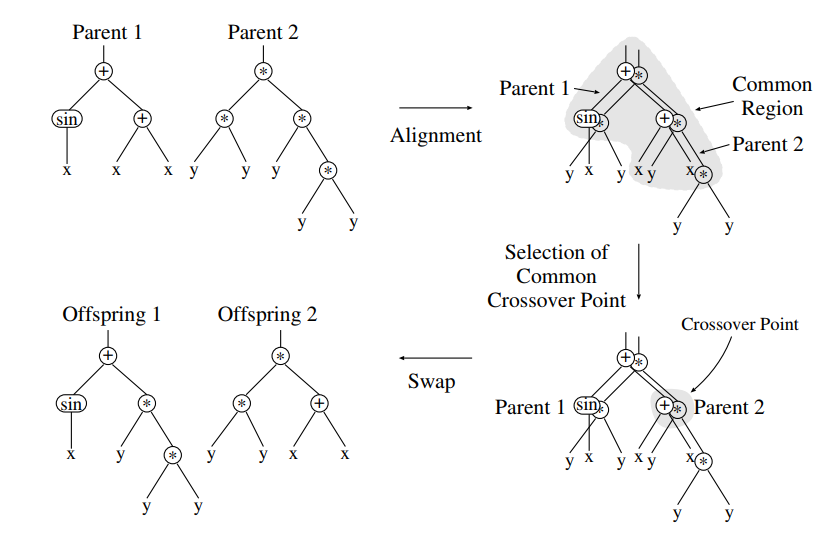
Endless Possibilities

The power of a Genetic Algorithm is its use of seemingly endless possibilities. The possibilities arise from two areas:

1) The depth of each program tree: more nodes → more functions → additional possibilities.
2) The number of generations it has to evolve.

I experimented with different maximum depths for the program trees, between 10 nodes deep to 15 nodes deep (1024-32,768 nodes). Surprisingly the change in the maximum depth of the nodes did not impact the final score. I now understand that after a certain depth, the randomness of the algorithm makes it hard for a large scale program to reach better results than smaller programs. There is always a chance that some random function in a specific node destroys all the calculation that was done below it, unfortunately the random switching done in mating just isn't a strong enough tool to remove all of these rogue nodes.

My initial thought when starting this project was that having large scale programs and have them evolve thousands of times will eventually create the optimal program to solve this game.



Reality

However, because the learning of a program is only done by randomly picking functions between its parents, without any understanding or learning what are mistakes, no great achievements were reached.



Results

My first attempt required the program to return the specific column in which it intends to put the curr_disc (modulo by 7, in order to insure the disc is inserted in a legal column(0-6)). The algorithm quickly entered a local optimum and never progressed. I believe that the randomness of the functions made for this sort of calculation to be extremely hard; considering how a simple +2 or -1 at the end of a program tree would change the final answer completely.

"All problems in computer science can be solved by another level of indirection."

David Wheeler

Instead, I required from the program to score each action (there are only 7 available actions each turn), and the highest scored action was the chosen one. This change, from choosing the correct action to just scoring each action, helped simplify the program to a simple + is good, - is bad.

The results showed a significant increase in score, and the end result was a gain of 2.3 rounds. Studying the best program in the final generation, it seems that the final score (~9) represents a basic understanding of the rules of the game. However no strategy/thinking ahead was achieved, it seems that for a truly great performance, a different approach should be taken.


Next Stage

The next stage will be to create a neural network, thus instead of random improvements, I'll try to use gradient decent with the idea that a more controlled evolution process would result in better results. A benchmark for success will be if the program would be able to beat my personal avg. score of ~13.





























References

[1]R. Poli, W. B. Langdon, and N. F. McPhee. A field guide to genetic programming. Published via http://lulu.com and freely available at http://www.gp-field-guide.org.uk, 2008. (With contributions by J. R. Koza); Figure 2.1, Page 10.
[2] Random was created using libsodium by Frank Denis Copyright © 2013-2017
[3]R. Poli, W. B. Langdon, and N. F. McPhee. A field guide to genetic programming. Published via http://lulu.com and freely available at http://www.gp-field-guide.org.uk, 2008. (With contributions by J. R. Koza); Figure 5.1, Page 45.